3.3 Kinetic Molecular Theory of Gases
Gurdit Sood
Assumptions for Ideal Gases
The Kinetic-Molecular Theory of Gases was created to explain the gas laws. It consists of five statements:
Gas molecules/atoms are small particles with mass but no volume in constant, random, straight-line motion
Gas molecules are separated by great distances, therefore the gas is mostly empty space.
Molecules collide only momentarily, and are not colliding most of the time.
There are assumed to be no forces between the molecules, except during collisions.
Individual molecules may gain or lose energy on collision, but the total energy is always constant.
Distribution of Molecular Speeds
Gas molecules may not move at the same speed. We cannot know the speed of the molecules because there are so many of them, but we can make predictions. The following equation is used to determine how many molecules are at a certain speed (u):
$$F(u) = 4 \pi (\frac{M}{2 \pi RT})^{\frac{3}{2}} u^2 e^{-\frac{Mu^2}{2RT}}$$
This is the Maxwell-Boltzmann equation, which describes the distribution of speeds in a gas. The derivation for this is not explained as a high level of math is needed, and you definitely DO NOT need to memorize this! The purpose of this equation in CHEM 112 is to help understand how the speeds depend on the molar mass (M), and temperature (T).
Figure 1 below depicts the plot of this equation. We can see that F starts from 0 and increases until it reaches a maximum point, and then it decreases as speed increases. This figure is important because it shows what the speeds of molecules are. The area under the curve also tells us the total number of molecules in the gas.
In this graph, there are also three speeds that are described: the probable speed (also commonly referred to as the modal speed), the average speed, and the root-mean-square speed. They all have expressions that can be used to calculate their speeds:
$$u_p = \sqrt{\frac{2RT}{M}} \text{\ or\ } \sqrt{\frac{2RT}{M}}$$
$$u_{av} = \sqrt{\frac{8RT}{\pi M}}$$
$$u_{rms} = \sqrt{\frac{3RT}{M}}$$
These expressions are derived by using calculus, please refer to the textbook to see them. It is important to note that these equations are useful as they relate u to M and T.
Altering the temperature of the gas (changing T) or its identity (changing M) will change the speed as we just saw, and thus flatten or compress the curve - flattening (or shifting to the right) means a greater proportion of molecules attain higher speeds, and occurs with increased temperatures. Compressing (or squishing it to the left) means more molecules slow down and have slower speeds, which happens when you cool a gas down.
Lastly, the distribution of molecular speeds can be shown experimentally using an apparatus. Please look at page 222 of the textbook, this is just for interest and is not tested in CHEM 112.
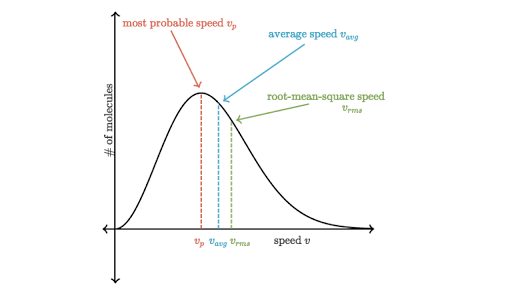
Figure 1: The Maxwell-Boltzmann distribution curve2
Temperature and Kinetic Energy
When looking at the kinetic energy of a particle, it is defined by the equation:
$$E_k = \frac{1}{2}mu^2$$
Where kinetic energy, $E_k$, is related to the mass ($m$) and speed (u) of the particle. However, when we have several particles, they are all moving at slightly varying speeds. Therefore, we can find the average kinetic energy of the particles. Given that all the particles are the same, we can replace mass ($m$) with $\frac{M}{N_A}$ (the mass of an individual atom). As for speed, we would replace u with urms. Now the equation would be:
$$E_k = \frac{1}{2} \cdot \frac{M}{N_A} \cdot (u_{rms})^2$$
Previously, it was determined that:
$$u_{rms} = \sqrt{\frac{3RT}{M}}$$
If we substitute this into the previous equation and simplify, we would end up with the following:
$$\overline{E_k} = \frac{1}{2} \cdot \frac{M}{N_A} \cdot (\sqrt{\frac{3RT}{M}})^2$$
$$\overline{E_k} = \frac{1}{2} \cdot \frac{M}{N_A} \cdot \frac{3RT}{M}$$
$$\overline{E_k} = \frac{1}{2} \cdot \frac{3RT}{N_A}$$
$$\overline{E_k} = \frac{3}{2} \cdot \frac{RT}{N_A}$$
With this final equation, both $R$ and $N_A$ are constants; therefore, we can conclude that temperature ($T$, measured in Kelvin) is directly proportional to the average translational kinetic energy of the molecules. This principle also applies to the pressure relationships with the ideal gas law. As temperature increases, the increase in kinetic energy causes an increase in collisions (increasing the collision force), which results in an increase in pressure.
References
Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:218-225.
What is the Maxwell-Boltzmann distribution? (article) | Khan Academy. Khan Academy. https://www.khanacademy.org/science/physics/thermodynamics/temp-kinetic-theory-ideal-gas-law/a/what-is-the-maxwell-boltzmann-distribution. Accessed September 1, 2022.