3.4 Gas Properties Relating to the Kinetic-Molecular Theory
Khoi Tran, Andy Lee
In order to better understand the movement of gases, we will be discussing two fundamental processes of gases, diffusion and effusion.1
Diffusion describes the net movement of molecules (in this case, of gases) due to the random motion of individual molecules. For example, in Figure 1, gas molecules (red dots) are initially localized in the top-left corner. Over time, random motion of these molecules will cause the gas to diffuse throughout the entire container, resulting in a homogenous environment.
Typically with diffusion, there are gases on both sides of the threshold (if one exists) or within the container, allowing for movement of the compound from higher to lower concentration with the help of collisions.
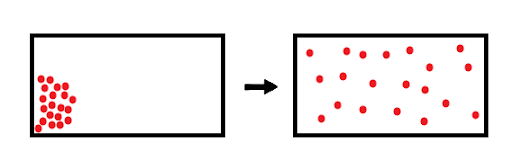
Figure 1: The diffusion of gas molecules inside a closed container.
Effusion is the escape of gas molecules from a container through a hole. Typically in effusion, a container on 1 side of the hole is empty (meaning no collisions occur), but there is still movement from high to low concentration.
Figure 2: The effusion of gas molecules through a small gap.
The rate of effusion of a gas through a small gap depends on the molar mass of the gas. The heavier the gas, the slower it effuses. Specifically, the rate of effusion of a gas is inversely proportional to the square root of its mass, or
$$\text{rate of effusion of A} = \frac{1}{\sqrt{M_A}} \text{\ (1)}$$
This is known as Graham’s Law.
From equation (1), we can establish a relationship between the molar masses of two gases and their respective rates of effusion: $$\frac{\text{rate of effusion of A}}{\text{rate of effusion of B}} = \frac{1/\sqrt{M_A}}{1/\sqrt{M_B}} = \sqrt{\frac{M_B}{M_A}} \text{\ (2)}$$
Furthermore, because the rate of effusion of a gas is directly proportional to its molecular speed, effusion time, distances traveled, and amounts of gas diffused, we also have: $$\frac{v_A}{v_B} = \frac{\text{effusion time of A}}{\text{effusion time of B}} = \frac{d_A}{d_B} = \frac{n_{\text{A diffused}}}{n_{\text{B diffused}}} = \sqrt{\frac{M_B}{M_A}} \text{\ (3)}$$
Remember that the identities of the gases in the fraction are flipped on opposite sides of the equal sign (Gas A is in the numerator on the left when comparing rates, and is in the denominator on the right when comparing molar masses).
Note: While the derivation for equation (1) might be introduced in lectures, it is not important for the purpose of CHEM 112. The lecture example also goes into more details than needed for assignments/assessments.
Non-Ideal Gases
Recall the equation relating the number of moles, temperature, pressure, and the volume of an ideal gas:
$$PV = nRT$$
This equation is based on the assumption that the volume of gas molecules is negligible, the molecules do not attract or repel each other, and that gas molecules do not lose energy when they collide.2
However, we live in a cruel society where none of these is really the case. Although gases behave quite ideally at high temperatures and low pressures (which allow gas molecules to move very fast while being far from each other), they tend to behave non-ideally at low temperatures and high pressures.
- High pressures: Specifically, the volume of gas molecules itself may cause the PV product to be higher than ideal when they are cramped together (high pressure), as gas molecules actually do have a volume they occupy.
- Low temperatures: Alternatively, intermolecular attractions may instead cause the PV product under low temperature to be lower than ideal, as the molecules will be much closer together than predicted by the kinetic-molecular theory.
The van der Waals equation
A revised version of the ideal gas law equation is developed by the Dutch scientist Johannes Diderik van der Waals, which accounts for the properties of different real gases.3
$$(P + \frac{n^2 a}{V^2})(V - nb) = nRT$$
In this equation, n is the number of moles of gas molecules, a and b are constants that are unique to different gases at different temperatures and pressures. A is specifically used to correct for the intermolecular attractions that gas molecules experience, and b is to correct for the non-zero volume that gas molecules occupy.
Practice Problems
Unable to continue with his outdoor research due to COVID-19 lockdown, out of boredom, Dr. Brzęczyszczykiewicz decides to inject 109.145 g of gaseous carbon dioxide into an empty 5.92 L pressure tank at 300.0 K.
a) He wants to try using the van der Waals equation that he learned years ago. Given $\ce{a = 3.658 bar \cdot L^2 \cdot mol^{-2}}$ and $\ce{b = 0.0429 L \cdot mol^{-1}}$, what is the pressure inside the pressure tank, in bar? Use $\ce{R = 0.08314 bar L mol^{-1} K^{-1}}$.
b) The pressure gauge indicates that the pressure inside the tank is 11.4 bar. This pressure gauge was manufactured by his NASA engineer friends and is very accurate. What is the percent error of the calculated pressure?
c) Which of the following may cause the calculated pressure to be lower than the actual pressure?
A - The valve of the pressure tank is faulty. The pressure inside the tank increases as the pressurized air rushes outside.
B - There is air remaining in the tank before carbon dioxide is added. The extra air exerts additional pressure inside the tank.
C - He assumes that the gas carbon dioxide behaves ideally and intermolecular attractions are negligible.
D - More than one of the above options.
Dmitri finds a pressure tank containing a mysterious gas when cleaning his basement. With his Bachelors of Science in Chemistry, he wants to identify this gas by determining its molar mass. He decides to blow up two identical balloons to 5.00 L, one with the unknown gas, and the other with carbon dioxide. These balloons are placed in a 300. K and 0.81 atm chamber. Overnight, the volume of the carbon dioxide balloon reduces to 3.80 L, while the unknown gas balloon reduces to 4.12 L. He knows that the unknown gas is a hydrogen halide with a form of HX, where X is a halogen. What is the chemical formula of the mystery gas?
Nelson is attempting to apply the ideal gas law to calculate an experimental value for the gas constant, R. To do this, he injects a fixed amount of helium into a specialized chamber of a fixed volume. He then records the pressure at different temperature points. He would then plot these data points onto a P vs nRT/V chart and use the slope to calculate the R. He calculates that his experimental R value is higher than the accepted value. Which of the following may have caused a high R value?
- A - He injects too much helium into the chamber. High amounts of helium causes P to increase and calculated R will be larger.
- B - He injects too much helium into the chamber. The pressure inside the chamber is too high, and the volume of the gas atoms become significant.
- C - The temperature inside the chamber is too low, which makes the London dispersion forces significant.
- D - The temperature inside the chamber is too low, making the term nRT/V smaller. This results in a larger R value.
- E - More than one of the above.
References
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson 2.Canada; 2017:225-226.
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:228-229.
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:229-230.