3.1 Introduction to Gases
Gurdit Sood
Understanding Pressure1
We all have heard of pressure before, but what is it exactly? Pressure is the force per unit area, or in other words, it is the distribution of force over an area. The unit of pressure is the newton (N - the force) over a unit area - in this case, the area is m2. Thus, pressure can be described by the following equation:
$$\text{Pressure (Pa)} = \frac{F(N)}{A(m^2)}$$
The pressure of one newton over a square meter is known as a pascal, but pascals are quite small quantities, so pressure is typically measured in kilopascals.
There are additional units for pressure that you may come across, so it is helpful to know the following conversions:
$$\text{101.325 kPa = 760 torr = 760 mmHg = 1.00 atm}$$
Simple Gas Laws1
If you recall from highschool, you have already covered the Simple Gas Laws, and so, we will briefly go through each law and highlight the main points. Before that, however, it is important to know one additional important property of gases, which states that a gas will occupy the volume of a container it is in (unlike solids or liquids, which have a fixed volume).
Boyle’s Law
When the amount of moles (or the amount of gas is another way to say this) and temperature is fixed, pressure is inversely related to volume. Meaning that as volume increases, pressure decreases. As pressure increases, volume decreases.
$$\text{Proportionality Statement:\ } \ce{P \propto 1/V}$$
Note: The “∝” is the proportionality symbol.
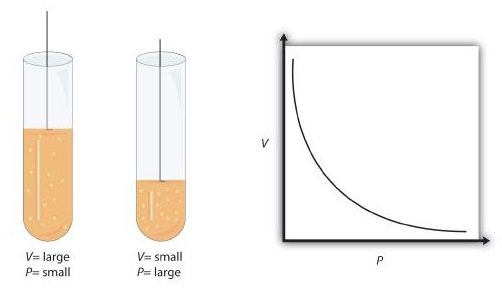
Figure 1: Visualizing Boyle's Law3
Charles’ Law
When the amount of gas (moles = n) and pressure (P) is fixed, the volume of the gas (L) is directly proportional to the temperature (measured in Kelvins - K) of the gas. As the temperature of the gas increases, the gas will begin to expand as the kinetic motion of the molecules increases, hence the space the gas occupies increases (increased volume).
$$\text{Proportionality Statement:\ } T \propto V$$
$$\text{Equation:\ } \frac{V_i}{T_i} = \frac{V_f}{T_f}$$
Knowing that P is proportional to 1/V, and V is proportional to T, it stands that P is also directly proportional to T. This relationship is known as Gay-Lussac’s Law.
$$\text{Proportionality Statement:}\ P \propto T$$
$$\text{Equation:\ } \frac{P_i}{T_i} = \frac{P_f}{T_f}$$
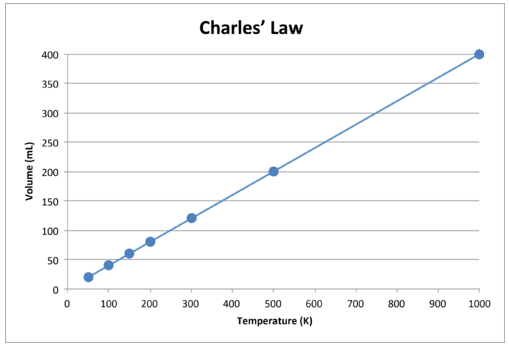
Figure 2: Visualizing Charles' Law4
Avogadro’s Law
When the temperature and pressure are set, the volume of the gas is directly proportional to the amount of gas present (in moles). If the amount of moles of gas increases, so does the volume of the gas.
$$\text{Proportionality Statement:\ } V \propto n$$
On a side note, this statement also indicates that at 1 mol of gas, there will be a constant volume occupied by the gas (assuming a constant temperature and pressure). Typically, this value is 22.4 L/mol - this can simplify problems greatly, as it is true regardless of the identity or molar mass of the gas.
The Ideal Gas Equation and the General Gas Equations5
When you combine the following gas laws:
- Boyle’s Law: $$V \propto \frac{1}{P}$$
- Charles’ Law: $$V \propto T$$
- Avogadro’s Law: $$V \propto n$$
You get this: $$V \propto \frac{nT}{P}$$
We can replace the “$\propto$” with “R”, which will be our proportionality constant.
$$V = \frac{RnT}{P}$$
Rearranging this equation, we get a equation we are quite familiar with:
$$PV = nRT$$
This is the ideal gas equation. When a gas has “ideal gas” behavior, this equation is used. When calculating using this equation, various R values can be substituted based on the units - the 3 most common constants to know are: 0.082 atm $\cdot$ L /mol $\cdot$ K, 8.314 kPa $\cdot$ L/mol $\cdot$ K, and 8.314 J/mol $\cdot$ K.
Real gases, however, do not conform to this behavior a lot, hence there is a need for a general gas equation.
$$\frac{P_i V_i}{n_i T_i} = \frac{P_f V_f}{n_f T_f}$$
The general gas equation is used when one or more properties of the gas are controlled, such as in this case, the amount of moles of gas is controlled. The general gas equation is typically used when the initial and final conditions of multiple variables have changed.
Practice Problems
- If the volume of the gas initially is 623 mL and has a temperature of 255°C, and has a final volume of 277 mL, what is the temperature?4
- Calculate the pressure (in kPa) caused by $1.00 \cdot 10^{20}$ molecules of a particular gas at 175°C and in a 305 mL container.
- What is the final pressure of a particular gas when its moles remain constant, and the initial pressure is 1 bar, the initial temperature is 273 K, and the final temperature is 373 K?
References
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:195-196.
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:201-205.
- Boyle’s Law Practice Problems. YouTube. https://www.youtube.com/watch?v=v8r_AU_TlPg. Published September 15, 2017. Accessed September 4, 2022.
- LibreTexts. 11.5: Charles’s Law: Volume and temperature. Chemistry LibreTexts. https://chem.libretexts.org/Courses/Eastern_Wyoming_College/EWC%3A_CHEM_1000_-Introductory_Chemistry%28Budhi%29/11%3A_Gases/11.05%3A_Charles%E2%80%99s_Law%3A_Volume_and_Temperature. Published August 11, 2020. Accessed September 4, 2022.
- Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:206-209.